Sum of the Interior Angles

Junior (Age 9 – 12)

Curriculum Goal

Junior: Geometry and Spatial Sense

  • Identify geometric properties of triangles and construct different types of triangles when given side or angle measurements.

Junior: Measurement

  • Use the properties of supplementary angles, complementary angles, opposite angles, and interior and exterior angles to solve for unknown angle measures.

Context

  • Group-based exploratory activity to explore the relationship between the sums of interior angles in different polygons.
Print Lesson
Appendix A
Appendix B
Appendix C
Appendix D

Materials

  • Chart paper with a triangle in the middle
  • Various hexagon cut-outs (Appendix A)
  • Printout with all hexagons on one page (Appendix B)
  • Heptagon and decagon (Appendix C)
  • Organization table (Appendix D)
  • Protractors (for students to check their work)
  • Markers

Lesson

  • Divide the class into six groups and provide each group with a piece of chart paper.
  • Have students discuss their pre-existing knowledge of angles and write down their thoughts. Encourage students to think about angles in the context of polygons.
    • Some students will remember that a triangle has three angles that add up to 180°. This fact is necessary to solve the next challenge.
    • Help groups that do not have that understanding by giving them several construction paper triangles. Demonstrate that by ripping off the corners of a triangle and placing them side-by-side with the vertices meeting at one point, the edge created is a straight line.
  • Introduce polygons (a closed figure with at least three straight sides and three angles) with visuals to support the instruction. Show examples, such as the triangle on their paper, and include relevant terminology (e.g., hexagon – polygon with six sides, interior angles – the angles that are inside the closed figure).
  • Distribute a hexagon cut-out (Appendix A) to each group. Tell students they will work together to find a strategy to determine the sum of its interior angles without a protractor.
    • Potential strategy: split the hexagon into triangles. Because a triangle’s interior angles add up to 180°, the sum of the hexagon’s interior angles is the number of triangles × 180°. This is also the case for the sum of the interior angles of a quadrilateral.
    • Ask groups that finish early to test out their method on the other groups’ hexagons.
  • Assist groups that are having difficulty. Strategies:
    • Ask, “How could you use your knowledge of the sum of angles in a triangle to help you solve this?”
    • If students are having difficulty using the polygons they have drawn inside their hexagon to find a solution, ask, “Do all of your drawn polygons’ internal angles also make up the hexagon’s interior angles? Is there a way you could make that so?”
    • Suggest they line their interior angles with a colour to help visualize the problem.
  • Invite groups to share the sum they determined, their strategy, and any problems they encountered.
    • Provide each group with a copy of Appendix B to help students visualize the angles while listening to their peers.
    • Students should recognize that every group had a hexagon with its interior angles totalling 720°.
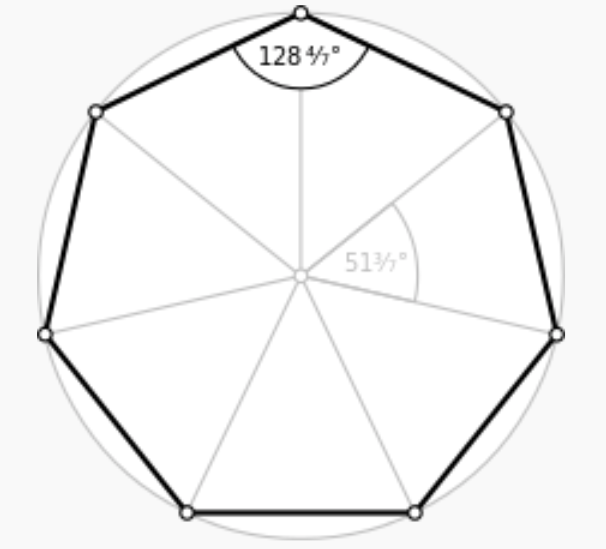
  • Repeat the exercise and discussion with heptagons and decagons (Appendix C). Remind students of their previous strategies to determine whether there is a pattern that allows them to find the solution for any polygon.
    • Ask struggling groups, “Do you notice a pattern between the number of sides in your polygon and the sum of its interior angles? How could that pattern help you find the sum of any polygon’s interior angles quickly?
    • Not all groups will arrive at the same understanding – listening to other groups and allow students to consolidate the concepts that have been explored.
  • Help students recognize patterns by inviting them to complete the organization table (Appendix D). Students can be provided the other polygons if needed.

Look Fors

  • Are students able to explain why the sum of a triangle’s corners is 180°? Do students use this knowledge to discover the sum of the angles in a hexagon?
  • Are students using any other strategies to understand the sum of the angles in a hexagon? How about heptagons and decagons?
  • Can students recognize the pattern between the number of sides in a polygon and the sum of its interior angles?

Extension

  • Have students use their pattern to write an algorithm that can be applied to any polygon to determine the sum of its interior angles.
Print Lesson
Appendix A
Appendix B
Appendix C
Appendix D

Share this lesson

Share on facebook
Share on twitter
Share on email