Thousands Blackjack

Curriculum Goal

Round whole numbers to the nearest ten, hundred, or thousand, in various contexts.
Use mental math strategies to multiply whole numbers by 10, 100, and 1000, divide whole numbers by 10, and add and subtract decimal tenths, and explain the strategies used.
Represent and solve problems involving the addition and subtraction of whole numbers that add up to no more than 10 000 and of decimal tenths, using appropriate tools and strategies, including algorithms.

Review math concepts, such as rounding, adding, and determining the reasonability of sums together with students. Clear up any outstanding questions and/or misconceptions.
Students play in small groups. Encourage discussion about strategy and communication about any of the mental math students are engaging in.
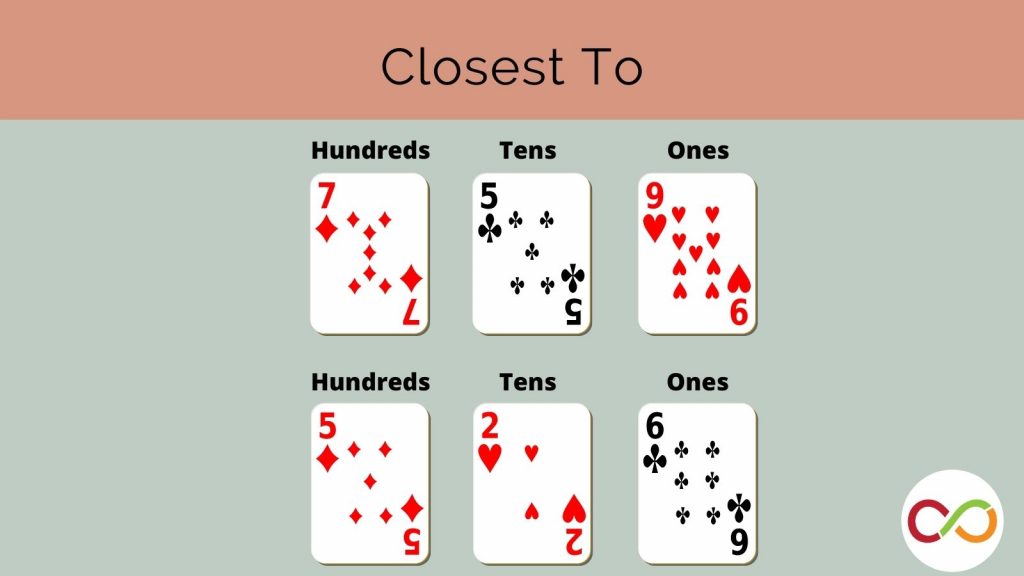
The goal of this game is to be the player who accumulates a set of cards with the sum closest to 2100.
One student is selected as the dealer and deals two cards to each player.
- At this point, players cannot write anything down to determine whether the sum of their two cards is near 2100.
- Express an understanding that determining the sum of a set of three-digit numbers is complex, so rounding numbers is encouraged.
The dealer offers additional cards to each player. Players can either: 1) Pass – they will not take any additional cards. Or, 2) Accept additional card until they think they are the closest to 2100.
When players have finished accepting additional cards, players can use paper/pencil to calculate their exact sum.
The dealer will verify the sums with a calculator and the player with the closest sum to 2100 wins the game.
Example questions to extend student thinking:
- What is your thinking behind accepting or refusing additional cards?
- Did you round your cards up or down? Did that influence your decisions? If so, how?
- Does your final sum seem reasonable?

Instead of being as close to 2100 as possible, the students must be as close to 2100 as possible without going over.
The game can be adapted to higher or lower sums, and even decimal sums, depending on curriculum expectations (Appendix A includes a page of blank cards).

Students use their knowledge of place value to arrange their cards to form the largest possible number.

21 requires students to accumulate cards with a sum as close to 21 without going over. Thousands Black Jack may be used as an extension to 21.