"Fibonacci" Sequence
Junior (Age 9 – 12)
Curriculum Goal
Junior: Patterning and Algebra
- Identify and describe repeating, growing, and shrinking patterns, including patterns found in
real-life contexts, and specify which growing patterns are linear. - Determine pattern rules and use them to extend patterns, make and justify predictions, and
identify missing elements in repeating, growing, and shrinking patterns.
Context
- Individual or group exploratory activity followed by a debrief, story, and art activity.
Materials
- Fibonacci slideshow (Appendix A)
- Fibonacci spiral sheets (1 for each student) (Appendix B)
- Large sheet of graph paper
- Pencil crayons and markers
Lesson
- Display the following number sequence on the projector: 0, 1, 1, 2, 3, 5, 8, 13 (Appendix A).
- Ask students to discuss the number sequence in small groups and determine the pattern rule.
- When students have identified the pattern rule, ask students to find the next three
terms in the sequence.
- When students have identified the pattern rule, ask students to find the next three
- Debrief as a class: This list consists of the first 8 terms in the “Fibonacci” sequence, where the
next number is found by adding up the two numbers before it.- If some students or groups are unable to determine the pattern rule, give them the
opportunity to find the next three terms in the “Fibonacci” sequence.
- If some students or groups are unable to determine the pattern rule, give them the
- Give students a brief history of the “Fibonacci” sequence.
- Note: The Robertson Program has chosen to place Fibonacci in quotes as per research by Rochelle Gutierrez.
- Share the following information with students: We place Fibonacci in quotes to
highlight the presence of settler colonialism. That is, although the Italian Leonardo Pisano (Fibonacci) receives credit for the pattern, many cultures and persons throughout the world had already known/performed the same pattern many years earlier. For example, the sequence is present in ancient Sanskrit texts that used the Hindu-Arabic numeral system in 200 BC, predating Leonardo of Pisa by centuries. In fact, if humans are no longer the center, we might credit Nautilus pompilius (Nautilus shell), Pinus coulteri (pinecone), or Helianthus annus (sunflower) with the “discovery” (p. 12, Footnote 6).
- Read Wild Fibonacci: Nature’s Secret Code Revealed or show the read aloud to your class. The read-aloud video is also embedded in Appendix A of this lesson.
- During the story, students will be introduced to the “Fibonacci” spiral, as pictured below.
- Tell students that the “Fibonacci” spiral is also known as the golden spiral.
- Ask students to share examples of how the golden spiral presents itself in animals
- Tell students that we will work together as a class to draw a Fibonacci rectangle and spiral using the Fibonacci sequence.
- Follow the script below to draw the Fibonacci rectangle at the front of the classroom on a large sheet of graph paper.
- What are the first two terms of the Fibonacci sequence?
- Once students have responded, colour in two 1 x 1 squares side-by-side on the graph paper. Use different colours for each square.
- What is the next term of the Fibonacci sequence? Remember the pattern rule!
- Once students have shared their answers, colour a 2 x 2 square on top of the first two squares (using a new colour).
- Notice that the length of the new square is double the length of the original squares, because 1 + 1 = 2.
- Ask students to share the next terms of the Fibonacci sequence and follow the instructions below as they respond.
- Using a new colour, draw a 3 x 3 square to the left of the existing rectangle.
- Ask students to identify the relationship between the new square and the last two squares.
- Using a new colour, draw a 5 x 5 square underneath the existing rectangle.
- Using a new colour, draw an 8 x 8 square to the right of the existing rectangle.
- Continue this process in a counterclockwise manner until you end up with a large Fibonacci rectangle resembling the image above. Each new square will have an edge that is the sum of the two previous squares.
- Using a black marker, draw a spiral that begins at the top left corner of the first two squares and follows the edges of the following squares.
- What are the first two terms of the Fibonacci sequence?
- Discuss the relationship between the “Fibonacci” sequence and the “Fibonacci”
rectangles/spiral.- Ask students to share what they noticed in the process of constructing a geometric
interpretation.
- Ask students to share what they noticed in the process of constructing a geometric
- Tell students that the golden spiral is found in art and photography, where the focal point of the picture lies at the center of the spiral.
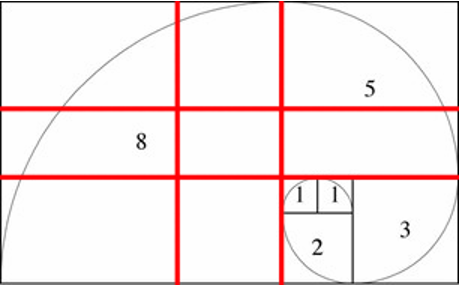
- Introduce students to the relationship between the golden ratio grid and the golden spiral, as seen in the image below.
- Share examples of the golden spiral in art and photography on the projector
(Appendix A). Ask students to determine the focal point in each of the images.
- Hand out sheets of paper with the Fibonacci spiral to every student (Appendix B) along with pencil crayons and markers.
- Students will create their own artwork that incorporates the Fibonacci rectangle or spiral on the
sheets of paper.- Students can take inspiration from objects in nature, famous paintings, or famous
photographs (Appendix A).
- Students can take inspiration from objects in nature, famous paintings, or famous
(elephant tusks, parrot beaks, alligator teeth, eagle talons, tiger claws, etc.).
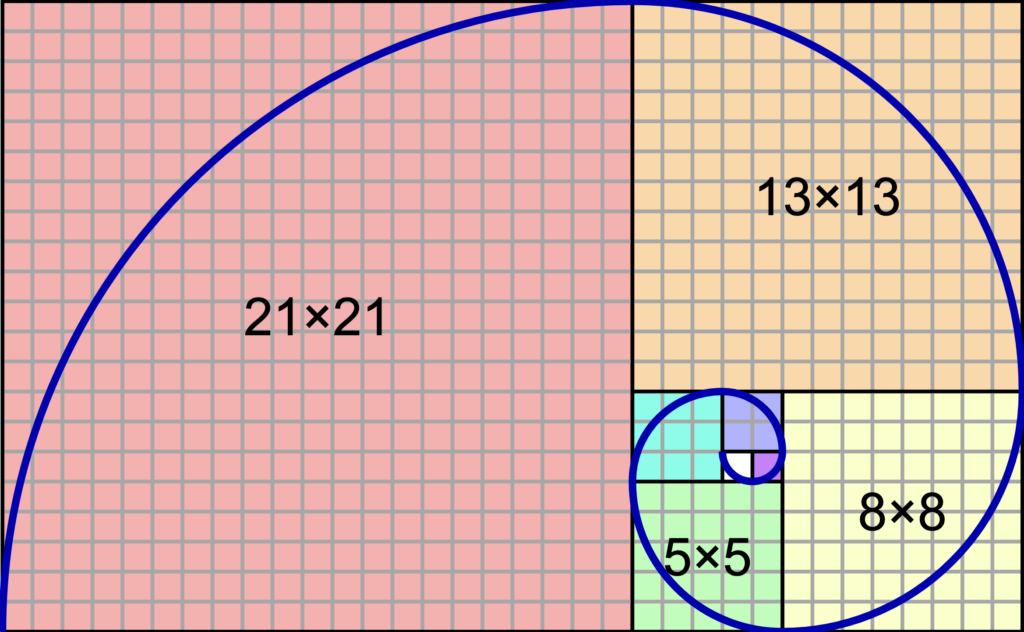
https://commons.wikimedia.org/wiki/File:FibonacciSpiral.svg#file
Look Fors
- Can students identify the pattern rule in the “Fibonacci” sequence? Can students find additional
terms of the sequence after determining the pattern rule? - Are students able to justify their observations regarding the pattern rule?
- Can students describe the ways that the Fibonacci sequence manifests itself in nature?
- What are the ways in which students incorporate the Fibonacci rectangle into their artwork?
Extension
- The golden spiral is found in art and photography, where the focal point of the picture lies at the center of the spiral.
- Introduce students to the relationship between the golden ratio grid and the golden spiral (shown to the right).
- Have students take one photo where the focal point is at the center of the spiral and one without the use of the spiral.
- The default camera apps on most Android phones have the golden ratio grid as a toggle in the settings. If not, the Open Camera app is a free alternative.
- iOS users can use the free Golden Ratio – Camera app.
- Compare photos and vote on which one is more aesthetically pleasing.
Note: The Robertson Program has chosen to place Fibonacci in quotes as per research by Rochelle Gutierrez:
I place Fibonacci in quotes to highlight the presence of settler colonialism. That is, although the Italian Leonardo Pisano (Fibonacci) receives credit for the pattern, many cultures and persons throughout the world, including Pingala in 200BC in India, had already known/performed the same pattern many years earlier. In fact, if humans are no longer the center, we might credit Nautilus pompilius (Nautilus shell), Pinus coulteri (pinecone), or Helianthus annus (sunflower) with the “discovery” (p. 12, Footnote 6).
Gutiérrez, R. (2017). Living mathematx: Towards a vision for the future. Philosophy of Mathematics 12 Education, 32(1).



