Metris: Multiplication + Tetris
Primary/Junior (Age 6 – 12)
Curriculum Goal
Primary: Number Sense
- Recall and demonstrate multiplication facts of 2, 5, and 10, and related division facts.
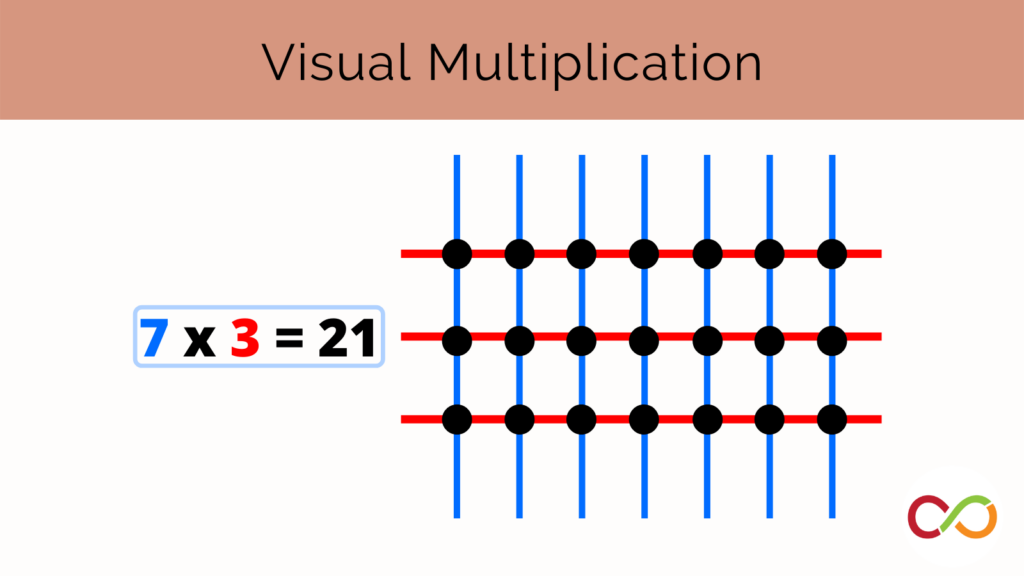
- Represent multiplication of numbers up to 10 × 10 and division up to 100 ÷ 10, using a variety of tools and drawings, including arrays
Junior: Number Sense
- Recall and demonstrate multiplication facts from 0 × 0 to 12 × 12, and related division
- Represent and solve problems involving the multiplication of two-digit whole numbers by two-digit whole numbers using the area model and using algorithms, as well as making connections between the two methods.
Junior: Geometry and Spatial Sense
- Use the row and column structure of an array to measure the areas of rectangles and to show that the area of any rectangle can be found by multiplying its side lengths.
Context
- Whole class instruction followed by students playing in pairs or groups no larger than 5 at their desk.
Materials
- Grid paper (larger sheets provide a better visual, but would take more time to colour)
- Different coloured markers/pencil crayons for each player
- Two dice per group (Four if students want to challenge themselves)
- Pencils, erasers, and scrap paper for rough work
Lesson
- Create a playing space on the grid paper (13 × 18 on a small sheet, customize accordingly for larger paper).
- Explain the objective and rules of the game:
- Player 1 will roll the dice to obtain the length and width of the rectangle they will draw (e.g., if a six and eight are rolled, the student may draw a rectangle that has a length of six squares and a width of three squares).
- If using four dice, Player 1 will roll two dice and add them together for the length. They will then roll the other two dice and add those together for the width.
- Player 1 will write the multiplication equation and solve it on their scrap paper (e.g., 6 × 3=18).
- If played as a collaborative game, Player 1 may ask for help from other players to solve the question. If no one can solve the question, the student must forfeit their rectangle.
- If played as a competitive game, Player 1 must solve the question individually. If they cannot solve it, Player 2 can choose to ‘steal’ that rectangle before having their own turn.
- Player 1 can draw their rectangle anywhere on the grid and colour it in.
- Players will take turns until the space is filled.
- Determine each player’s total area: the player with the most filled spaces wins.
- Player 1 will roll the dice to obtain the length and width of the rectangle they will draw (e.g., if a six and eight are rolled, the student may draw a rectangle that has a length of six squares and a width of three squares).
Look Fors
- What strategies do students use to fill the space? Do they start in the corners, sides, or middle of the space (spatial sense)?
- How quickly can students calculate the area of the rectangle and what strategies do they use to find the answer (e.g., use of mental math, manipulatives, counting, etc.)?
- Do students challenge themselves by incorporating all four dice? What challenges do they experience?
Share this lesson
Share on facebook
Share on twitter
Share on email