Whole Number Bias and 3 Misconceptions about Fractions in Junior Math
Whole Number Bias and 3 Misconceptions about Fractions in Junior Math
Q&A: OISE Assistant Professor Dr. Zack Hawes explains how whole number comprehension misinforms the comprehension of fractions
What is whole number bias?
Whole number bias is the tendency to apply or misapply one’s understanding of whole numbers or natural numbers – the numbers we typically count with – to rational numbers. It makes sense that people might apply what they have learned about whole numbers, like 1, 2, 3, 4 and 5 to their understanding of fractions, but unfortunately this leads to all kinds of misunderstandings about fractions. For example, people will incorrectly state that one quarter (1/4) is larger than one third (1/3). This demonstrates a failure to grasp the relationship between the two fractions, relying instead on the understanding that four is larger than three.
A&W knows this first hand. In the 1980s, the fast-food restaurant introduced a new third-pound burger to its menu, intended to rival competitor McDonald’s popular Quarter Pounder burger. A&W sold it at the same price as the Quarter Pounder, thinking they could win customers by offering more burger for the customer’s buck. But it didn’t catch on and when A&W held focus groups to determine what the problem was, they learned that people aren’t so savvy about fractions. More than half the focus group questioned the price of the third-pounder, wanting to know why they should pay the same price for a third of a pound as they did for a quarter of pound at McDonald’s. They believed A&W was overcharging them. So, it’s not just students who have difficulty grasping fractions.
VIDEO: In the 1980s, A&W tried to compete with McDonald’s Quarter Pounder by offering a ⅓ lb. burger at the same price. Confused consumers wrongly assumed that ¼ was bigger than ⅓ , resulting in a marketing fail. In 2021, they reintroduced the burger. This time, calling it the 3/9 burger.
One major obstacle is the symbolization of fractions and recognizing that they have a single magnitude in the same way as whole numbers. People see a fraction as representing two separate whole or natural numbers. They don’t conceive of the fraction as a single number with a magnitude that can be ordered, compared, and operated on like whole numbers. Let’s use one third as an example again, people may look at it and simply see a one over a three. They see the fraction as two individual numbers rather than one single number that could – and does – occupy a position on a number line, again like any whole number or natural number can.
We’re used to seeing the numerator and the denominator without processing that there’s a weight to that symbol, to that fraction. When we see 99, we’ve developed an understanding of its weight. Can you look at 9/11ths and have an immediate feeling for the weight of this magnitude? That is the challenge: getting people to instantly access the weight or the magnitude of a fraction in the same way that we do with whole numbers. Learning to do so would make it obvious that a third pound burger is a better deal than a quarter pounder.
Why is it important to use accurate language with fractions?
When talking about fractions, adults will say one over three when they’re actually talking about a third. When we say one over three, we’re using the language we use when we talk about whole numbers and applying it to fractions. That’s the whole number bias again. We’re using our knowledge of natural, counting numbers and attaching it to how we name and reason with symbolic fractions. So, the more we use accurate language like a third or an eighth, it shifts the focus to the correct meaning of the fraction.
Is there anything that can help with teaching fractions?
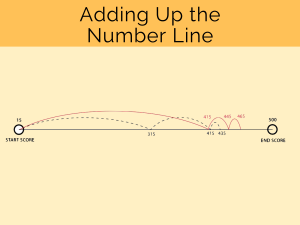
The number line is a really powerful tool for understanding fractions because it allows students to see that fractions really do occupy a single location on the line. It also allows students to see that multiple fraction representations can occupy the same position; they’re equivalent fractions.
While 33%, 0.33 and one third may appear to be different, they are of the same value and have the same magnitude so they lie in the same position on the number line. Now, we have an opportunity to discuss the relationship between percentages, decimals and ratios instead of approaching them as separate entities. Again, we see the importance of relationships here and learning to see the different ways we might code, symbolize, map, and represent different proportional relationships.
One of the simplest, yet most effective challenges you can pose to your students is to order fractions along a number line from smallest to largest. It seems simple, but it allows an educator to observe how a student is comprehending how fractions relate to one another. For example, students may not put two equivalent fractions underneath one another to show that they’re equivalent. Again, it’s because they’re used to dealing with whole numbers occupying the same position. Instead, you might observe that students reason about the “part that’s left over.” For example, when comparing seven eighths and eight ninths, students may consider them to be equivalent because the two fractions are each missing one part. With a number line, you can immediately see that they remember something about the missing part, but they’re not comprehending the equivalent weight of the two fractions.
In addition to visualizing and ordering fractions along a number line, it’s also important to have many opportunities to compare fractions. We know it is important to have young children compare whole numbers, and I think the same thing can be said about children’s initial learning of fractions. Games such as Fractions War, for example, where children compare and state the larger of smaller of two fractions, provides great opportunity to discuss the magnitude of fractions.
The number line helps model the connection between measurement (space) and number. It is flexible and makes conceptual understanding visible, including any error. Use this assessment to help determine how accurately students identify specific numeric locations on a number line.
Even before we introduce symbolic fractions, such as 2/5ths, we might consider having students first compare non-symbolic fractions and work towards developing a better understanding of what the symbolic notations of fractions represent.
I also can’t recommend enough the Fraction Talks website. Fraction talks is full of really great provocations and conversation starters, as well as a whole series of fraction lessons and activities, to get students thinking about fractions. Fractions Learning Pathways is another great resource that provides a really nice developmental sequence of instructional theory and activities.
The 3 misconceptions
1. Algorithms must be used to solve fraction problems
Grade 6 Teacher Ben Peebles explains how students often get hung up on “using the correct algorithm” to solve a fraction problem when they should focus on what the question is really asking of them.
2. A larger denominator means a larger number
Grade 5 Teacher Zoe Donoahue explains how her students create a fraction kit to help them understand the value of fractions and how they relate.
3. Fractions with different denominators don't relate
Grade 5 Teacher Zoe Donoahue explains how she leads classroom discussions to aid student comprehension of equivalent fractions.
Robertson Fraction Activities
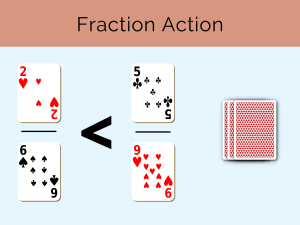
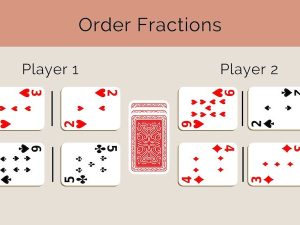
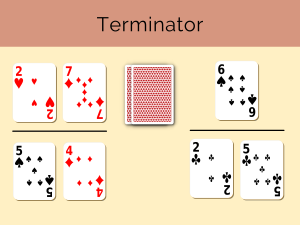
Students work with an assortment of cards from a standard 52-card deck, to create whole factions using addition.
Thank you to the Dr. Eric Jackman Institute of Child Study Laboratory School and its teachers for welcoming us into classrooms to learn about exemplary practices for teaching math and science. Thank you, as well, to Dr. Zack Hawes for sharing his insight on fractions.