Focus on Symmetry
Symmetry is a concept with wide-ranging applications in the natural and cultural worlds we inhabit. Pervasive in the arts, it serves as a foundational idea in STEAM areas, connecting complex mathematical concepts and driving theories in physics, chemistry and biology. Its manifestations are ubiquitous both in nature and in humanly built environments throughout history. The earliest known stone tools, bifacial hand-axes dating back 1.5 million years, are symmetrical; archaeologists suggest that from the start there may have been aesthetic considerations that transcended practical usefulness. Developmentally, the tendency of very young infants to preferentially attend to examples of bilateral symmetry (such as faces) soon develops into an explicit preference for symmetrical figures, a preference that spans societies across the globe.
Concepts of symmetry also apply to the social world. Children’s preoccupation with fairness – from even distribution of goods to fair teams in sports to sophisticated social justice considerations – is one obvious example.
Despite the importance of the concept in so many areas and at so many levels of complexity, and despite the evident interest it holds for students of all ages, symmetry remains a relatively underdeveloped area of study in elementary school curricula. When introduced, it tends to be a rather mechanical and static concept, often offered more as a kind of arts and crafts novelty (e.g, folding paper to create random paint blot designs or colouring in pre-drawn outlines of butterflies) than as a richly generative mathematical principle.
What is Symmetry?
The word “symmetry” (Gr. symmetria) originates in two Greek terms: syn (together), and metron (measure), suggesting ideas of balance and harmony that go beyond mere sameness. A two-dimensional form is considered symmetrical if it remains invariant when subjected to a basic spatial transformation, such as rotation around a point (radial symmetry; e.g., flower petals or snowflakes), lateral translation across a plane (tessellation; e.g., beehive or Islamic tiling), or reflection (mirroring) along an axis (e.g., butterfly). Such a definition is dynamic rather than static; it incorporates essential ideas of motion that raise interesting questions for children. For example, how does reflection relate to rotation? Under how many different angle rotations can a given figure remain unchanged? What happens to a configuration when you combine rotation and translation? How many axes of symmetry can co-exist in a single design? Which features of a design are essential to its symmetry and which are peripheral? How might all this play out in three dimensions?
Working with symmetry as a dynamic phenomenon encourages the kind of visualizing and mental rotation that builds scientific and mathematical thinking.
Symmetry in Play and Development
The early predisposition to recognize bilateral symmetry along a vertical axis likely originates in the symmetry exhibited by most living things. We come to know what it feels like to be a more-or-less (but not perfectly) symmetrical body in the world. Interestingly, it generally takes longer for children to recognize or create mirror symmetries across non-vertical axes.
The drive for symmetry is already apparent in the play of young children, who show growing inclination and ability to create spatially regular and patterned forms with art or construction materials and will often persevere to an astonishing degree to select the precise block needed to maintain the symmetry of a construction. Watching a child as they purposefully move around their building, carefully mirroring the placement of each element, clearly shows the deep embedding of math ideas in the body and its motions.
Remarking on the “very, very strong recognition and pull toward symmetry” exhibited by almost all her kindergarteners, Carol Stephenson suggests that a consistent absence of such understanding may appear alongside other developmental anomalies and raise a red flag for teachers. At the same time, it’s important to note the difference between the intentional creation of asymmetry (such as it appears in modern architecture and design), which consciously subverts or plays with the rules governing symmetry, and a young child’s pre-symmetrical production that has been randomly thrown together without awareness.
Children’s intuitive understanding is further developed when a teacher draws attention to salient features of their productions and invites them to explain their choices. Using the vocabulary of symmetry to describe a creation helps to make explicit the underlying ideas implicit in its construction. Focusing on the transformative possibilities of motion further challenges children to shift their productions so as, for example, to rotate a vertical line of symmetry into an oblique or horizontal one. Instruction of this sort often triggers an explosion of complex symmetries in both formal and informal classroom settings, spurring a mutually enriching cycle in which children explore and expand upon instructional ideas in play, which sets the stage for further instruction, and so on.
Carol finds the rapid development of skills, ideas and motivation emerging from the interplay of autonomous exploration and responsive instruction can lead even young children to perform well beyond what research leads us to expect, as they gleefully master radial symmetry and spontaneously mirror patterns across multiple non-vertical axes.
Symmetry in the classroom

A kindergarten student uses a cookie sheet and magnetic pattern blocks to create symmetry.

“It’s kind of a rainbow. Don’t you think it’s beautiful?” A junior kindergarten student creates rotational symmetry with perler beads.
A kindergarten student from Big Grassy First Nation shows educator Carol Stephenson her symmetrical design, which features rotational symmetry.
Spatial Reasoning
Spatial imagination plays a powerful role in scientific and mathematical understanding. A wide range of engaging symmetry activities, such as those offered on the Robertson website or in Taking Shape: Activities to Develop Geometric and Spatial Thinking (Moss et al., 2016), support its development. These include symmetry games in which players mirror one another’s growing designs as well as various explorations of symmetry in the world, identifying symmetries and asymmetries in letters and numerals, items in nature, or architectural examples.
One genre with rich possibilities is paper-folding and cutting, which builds fine-motor precision along with related geometric and numerical insights. The possibilities of paper-folding/cutting go well beyond the pleasing snowflakes that adorn classroom windows. They encompass a vast array of cultural art-forms ranging from Japanese Origami to elaborate paper-cutting traditions in Europe, South and East Asia, and Latin America . Building upon and subverting some of these traditions, contemporary artists such as Kara Walker express ideas related to racial and gender identity and violence through the evocative use of cut out silhouettes of black paper.
The Robertson team has carried out a series of activities in which holes are punched into variously folded pieces of paper and predictions made about the results when unfolded. Many teachers who have tried these activities in classrooms find themselves impressed and humbled by their students’ adeptness and their own fumbling!
The hole-punch challenges offer an abstracted version of the extraordinary symmetries produced in Indigenous traditions of birchbark biting – see curriculum ideas based on Micmac or Cree/Ojibway practices. The mathematics of Indigenous paper-folding is beautifully brought out in videos produced for the Math in a Cultural Context (MCC) program at the University of Alaska. Principles of fractions, proportional reasoning, doubling and halving and a great deal more come to light in the teacher’s compelling demonstrations of traditional Yupik approaches to real-world geometric problems.
Symmetry and Number
Exploring symmetry through paper-folding brings out essential ties between spatial and numerical understanding at the elementary level. Through this lens we recognize the inherent symmetry in even numbers and the asymmetry of odd ones. The idea of balance that defines equations and concepts of equality also speaks to a deep-seated symmetry which goes beyond surface differences to capture what is essentially the same about both sides of an equation such as 2 + 3 = 10 – 4 – 1. Commutativity is another symmetrical concept, as is the symmetricality of inverse operations such as multiplication/division or addition/subtraction.
Adults more easily identify the midpoint between a negative and positive number when the numbers are more symmetric around zero. Based on this finding, a more recent study (Tsang et al., 2015) rendered the abstractness of negative integers accessible to fourth-graders through the use of a symmetrical number line in which negative numbers and their positive counterparts were depicted as equidistant from a central point of zero.
Using a hinged number line that could be folded at the zero point, children recruited their intuitive perceptual grasp of visual symmetry to play a variety of games involving operations with positive and negative numbers. The researchers found that students easily applied and extended this approach when solving unfamiliar problem types involving negative fractions, pre-algebra challenges and word problems. They conclude that “emphasizing symmetry structure early may help prepare students to learn more difficult math topics in the future” (p. 183).
Spatial Resources
Spatial activities categorized by process, such as mental rotation, perspective taking, visualization and mapping.
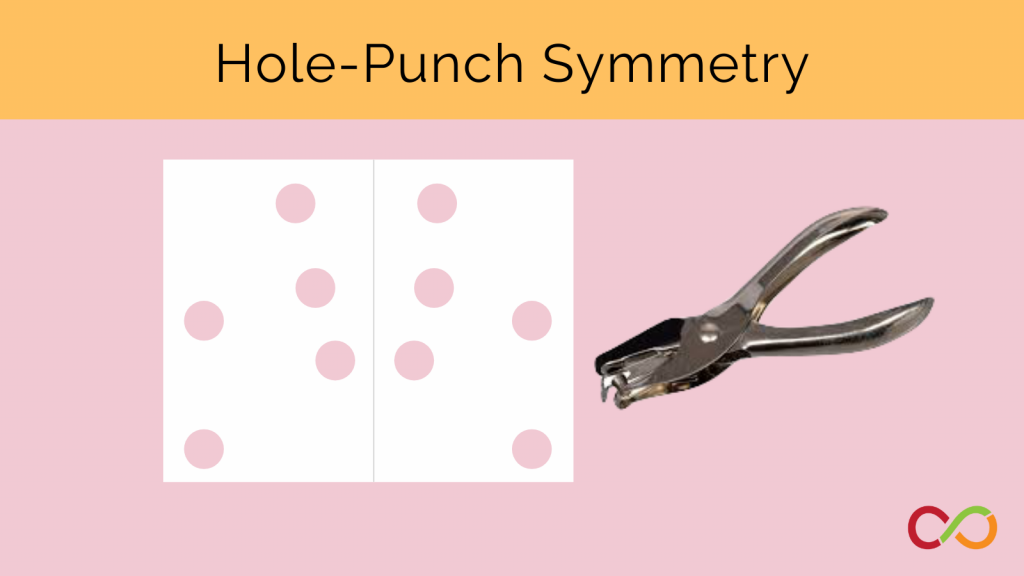
Students visualize how folded and hole-punched paper will look when unfolded.
Video: Birch Bark Biting
Elder Nora Atlookan explains in Anishinaabemowin how her mother created designs through birch bark biting.
Video: Symmetry and Number
A student in Raadiyah Nazeem’s Grade 1 class demonstrates an understanding of a possible relationship between symmetry and number.
Using Technology to Explore Transformations and Symmetry
While pretty much any physical material can lend itself to creating symmetries, the dynamic nature of the concept may be more extensively explored through computer applications such as Geometer’s Sketchpad that allow for systematic experimentation with geometric motion in space and enable transformations less easily achieved through physical manipulations.
One example is the work of Ng and Sinclair (2015), who used a digital technology platform to broaden children’s understanding of reflection beyond the static identification of symmetry and asymmetry. Using a ”symmetry machine”, students came to grasp the concept of symmetry dynamically as a kind of function or transformation. Another example is found in Seidel’s 1998 account, Tech Time: Symmetry in Season, which describes her experiences teaching the rotational symmetry of snowflakes to fifth-graders using Geometer’s Sketchpad. A growing understanding of angles and transformations allowed them to design their own rotationally complex snowflakes.
Try the technology
Geometer’s Sketchpad is a student-friendly computer application that integrates mathematics and technology to produce visual representations of math.
Importance of Symmetry
In short, there are sound reasons to capitalize upon children’s powerful instincts around symmetry in elementary math classrooms. Among other things, a focus on symmetry
- grounds learning in bodily experience and knowledge
- offers a route into understanding that speaks to common perceptual experiences and predispositions
- draws connections with cultural forms and modes of expression across the world
- develops critical understanding of space and number, and how the two come together
- sets the stage for later learning in math and science
- encourages multiple expressions of understanding
- provides opportunities for play, creativity and exploring the aesthetic side of math
- offers an organizing lens on the natural world
The potential of symmetry as a comprehensive organizing concept in mathematics comes out brilliantly in a 2019 paper that shares insights based on years of collaboration between educational researchers and Indigenous knowledge keepers in Alaska and Micronesia. The authors describe how they developed a mathematics education program based upon the centrality of symmetry in the culture.
“Symmetry and measuring act as an underlying cultural code connecting a wide array of activities and systematizing epistemologies Yet, the geometrical principles… that they employ transcend their cultural groups and can be applied widely to education. On the basis of numerous practical examples, we began to see how an analogous way of thinking about symmetry could be used as a fundamental framework for teaching school mathematics. We used these underlying mathematical principles to model how these processes can be cohesively applied to teach numbers, geometry, measuring, and early algebraic thinking. The elders’ potential contribution to the learning and understanding of mathematics is their view of symmetry and measuring as a centerpiece, an integrative, creative, and constructive process.” (Lipka et al., 2019)
Additional Resources

The 2021 Rosenthal Prize for Innovation and Inspiration in Math Teaching from the Museum of Mathematics explores the math possibilities behind creating a tessellation from an envelope.

A collaboration between the Faculties of Mathematics and Education at the University of Cambridge, this online database has 70+ symmetry activities, along with many more math resources.

Mathcurious creates math-focused learning activities, resources, books, and games. In this blog post, they suggest many ways to explore symmetry with children outside.
References
Lipka, J., Adams, B., Wong, M., Koester, D., and Francois, K. (2019). Symmetry and measuring: Ways to teach the foundations of mathematics inspired by Yupiaq elders, Journal of Humanistic Mathematics, 9 (1), pp. 107-157. Available at: https://scholarship.claremont.edu/jhm/vol9/iss1/7
Moss, J., Bruce, C., Caswell, B., Flynn, T. & Hawes, Z. (2016). Taking shape: Activities to develop geometric and spatial thinking. Pearson.
Ng, O-L. & Sinclair, N. (2015). Young children’s reasoning about symmetry in a dynamic geometry environment. ZDM Mathematics Education, 27, 421-434.
Seidel, J.D. (1998). Tech time: Symmetry in season. Teaching Children Mathematics, 4(5), 244-249.
Tsang, J.M., Blair, K., Bofferding, L. & Schwartz, D.L. (2015). Learning to “see” less than nothing: Putting perceptual skills to work for learning numerical structure. Cognition and Instruction, 33:2, 154-197.
Author

Dr. Julie Comay
Robertson Education Specialist, Professor (OISE/U of T), Former Classroom Teacher