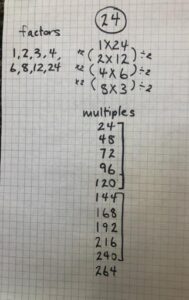Junior Daily Math Discussion

Grade 4/5 Teacher Zoe Donoahue shares how she reinvented
a primary daily math practice so it met the needs of her junior students

When I moved to teaching grade 5, I challenged myself to re-invent the Daily Math Discussion (DMD) that I had developed over many years of teaching in the primary division. The discussion evolved from the ubiquitous “calendar” routine common in many early years and primary classrooms into a robust discussion that gave children daily practise with many math concepts. I was determined to make the math discussion work for both the curricular demands and developmental stage of my junior learners.

Supporting Math Discourse and an Inquiry Approach

The DMD is an inquiry-based routine that encourages mathematical discourse. I aim to create a space where children can theorize, share their strategies, find patterns, see relationships, and appreciate that there are many ways to get to the answer. Children are often asked “How do you know?” and are supported to explain their strategies so that their classmates can understand their thinking. I refrain from repeating what children say, so that children understand that they need to listen to each other.

If I feel a child’s comment is hard for others to understand, I may ask them to elaborate or I may verify that I am understanding by asking, “Are you saying that…?” Another helpful practice is to write on the whiteboard as children explain a strategy or a theory so their thinking is made more visible to all.

There are several models and tools I use to make children’s thinking visible or to teach or reinforce concepts. Organizing data in ways that help children see patterns and relationships is important and can be framed for children as something that mathematicians love to do.

The open number line is a helpful way to see relationships between whole numbers, decimals, fractions or percents. Diagrams that show things like fractional parts are helpful (Fig 1). Showing both conventional algorithms and invented strategies, often beside each other, can also be very illuminating.

A consideration when working on math concepts in a discourse and inquiry-based way is what to do when children’s answers are incorrect. My approach is to record the incorrect answer and have the child explain their thinking, which often results in the child seeing where they have gone astray. At times, I may need to help with this process. Paramount during the DMD, and in all my teaching, is to create a safe space where children can take risks, theorize, and share their thinking and strategies, and to know that they will be supported by both me and by their classmates. We talk a lot about the opportunities that mistakes give us to learn and grow our understanding. We can also model this by asking children to address the mistakes we teachers make with kindness and respect.

(Fig. 1) Using an open number line is a helpful way to see relationships between whole numbers, decimals, fractions or percents. Diagrams showing fractional parts also help.

Differentiation

For the DMD to be effective, we must create a space where children who have different levels of skill and confidence as math learners can participate in a way that feels good to them. It’s important that the stronger math students don’t dominate. Giving adequate wait time (Mary Budd Rowe, 1972) can give children who are less confident or who need more time to process their ideas more time to think. Asking for several children to explain a strategy or their thinking can help children who may offer to speak only after they’ve heard several other children’s ideas. As well, different strategies may resonate with particular children. Most importantly, working with the same concepts day after day can build knowledge and skills and, I hope, lead to children feeling comfortable and wanting to participate. Children are continually exposed to concepts, rather than limiting them to math units that may be forgotten once a new topic is introduced.

Another benefit of this discourse-based routine is the development of mental math skills. Children are forced to move away from pencil and paper calculations and traditional algorithms, which are also important, and to move toward strategies where they work in their heads, often decomposing numbers and working in ways that might be more meaningful. For example, preserving place value by working left to right.

The joy and engagement that my students bring to this routine and the growth in mental math skills, mathematical discourse, and understanding of many math concepts, has made the Daily Math Discussion a cornerstone of my junior grade math program.

A year-round focus on factors

When I held the DMD in the primary grades, the centrepiece was a number line structured in rows of 10. Each day we added a number to the number line that corresponded to the number of days we had been at school. I thought this would also be an appropriate structure for my grade 5s but I have shifted the focus from skip counting to determining all the factors of the day’s number. After finding pairs of factors, written as multiplication equations, we list the factors in order (Fig. 2). The beauty of working with an ascending number line is that we start with easy numbers and build toward higher numbers.

Work with factors naturally leads to learning about prime and composite numbers. As we see where prime numbers fall on the number line, children theorize that they might be close to numbers that have many factors. For example, they may theorize that 23 is a prime number, coming just before 24, which has 10 factors. As we move through square numbers, such as 4, 9, 16 and 25, children realize these special numbers always have an odd number of factors, as one pair of factors is a number multiplied by itself.

(Fig. 2) After finding pairs of factors, written as multiplications equations, the Grade 4/5 class lists the factors in order.

At day 12, I introduce the foundational concept of doubling and halving. I write the factor pairs 2 x 6 and 4 x 3 above and below each other and ask the children if they see any relationship between the numbers. We establish a “times 2” or “doubling” relationship between 2 and 4 and a “divided by 2” or “halving” relationship between 6 and 3. Understanding the concept of doubling and halving becomes increasingly useful as we move to working with larger numbers.

Divisibility rules come into play as we explore factors. Children start to develop theories that we can work with and test out from day-to-day. For example, they may theorize that:

Even numbers are always divisible by 2,
Numbers ending in 5 and 0 are always divisible by 5, or
Odd numbers are only divisible by odd numbers.

Children may know or can be taught the divisibility rule for 3: a number is divisible by 3 if the sum of the digits is divisible by 3. Children may then theorize that all numbers in the counting by 9s pattern are also in the counting by 3s pattern, so the divisibility rule is similar.

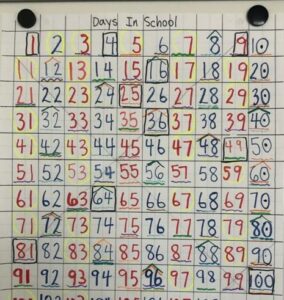
(Fig. 3) The Grade 4/5 students continue to list factors, while also “doubling and halving” skills to identify prime and composite numbers.

The numbers on the Days in School chart are written in a red/blue pattern so that odd and even numbers are highlighted (Fig. 4). Children observe that odd and even numbers are in the columns and will see many skip counting patterns. For example:

Numbers in the counting by 11s pattern are in a diagonal line from left to right and are in an odd/even pattern,
Numbers in the counting by 9s pattern are diagonal from right to left and are also in an odd/even pattern, or
Numbers in the counting by 4s pattern are always even and present in a checkerboard pattern

To highlight these patterns further, we mark the skip counting patterns in a particular way, including a squiggly purple line under the multiples of 3, a green point over the multiples of 8, and a diagonal line through the numbers in the 9s and 11s patterns (Fig. 5). These symbols help us to see how many factors each number has, and allow us to identify prime numbers, which we indicate with a yellow circle. This year, the children suggested we also mark the square numbers with a square. This growing number line becomes a reference that children use when working on other math assignments. It is an anchor for much of our work together and a growing record of our learning.

I was thrilled to see my Grade 5s just as excited as my Grade 1s when a number has a lot of factors. My students were surprised that a number as low as 12 could have 6 factors. As we moved into the 20s and 30s, they began to theorize that all numbers that are multiples of 12 have many factors. Some wondered whether every number that is a multiple of 12 would also include all the factors of 12 – 1, 2, 3, 4, 6, 12. When we got to 60, which has 10 factors, the children were excited that the factors included consecutive numbers 1, 2, 3, 4, 5, and 6. They then theorized that 120 (or 2 x 60) might also be a number with a large number of factors.

(Figs. 4 & 5) The numbers on the Days in School chart are written in a red/blue pattern so that odd and even numbers are highlighted. Additional markings are added, such as squiggly lines and diagonal lines to illustrate additional patterns.

Detailed DMD monthly breakdown

Zoe strategically introduces different mathematical concepts as the school year progresses. Below, Zoe provides insight on why she introduces concepts at that time of year and gives examples of how her students engaged at the time.

September/October: Multiples

There is a second focus in addition to our year-long work on factors that is explored for about two months. The first topic we explore is multiples of the days in school number. I record multiples that the children suggest in a way that patterns in the ones, tens, and hundreds columns become apparent. In the image to the right, children noticed that on Day 19, the numbers in the ones column were counting down by 1s and the numbers in tens and hundreds columns were counting forwards by 2s until 190. They also noticed that this pattern resumed at 209 and noted that there is an odd/even pattern when counting 19s that is very similar to a pattern they noticed when counting by 9s.

November/December: Division

A second focus on division begins around the beginning of November. We use the number of the day and systematically divide it by numbers 1 to 10. The goal is to identify the equations that yield whole numbers, which connects directly to our work with factors.

When equations do not result in a whole number, I express remainders in both whole number and fraction form. The language I use is very purposeful to help frame what I want children to learn from this work. Because we so often work with numbers where there will be a remainder. I might ask, “How many times does 3 go into 20?” or “What number could we multiply 3 by to get to 20 or close to 20 without going over?” Children use their knowledge of times tables and trial and error to determine that 3 x 6 is 18 with a remainder of 2. Thus, the answer is 6 R2 or 6 2/3. Working with fractional remainders also provides practise reducing fractions to their lowest terms and builds knowledge of equivalent fractions.

Working with consecutive numbers, children start to see patterns and relationships. For example, they recognize that all numbers between 17 and 23 are not divisible by 8, but that 24 (8 x 3) will be. There are often some neat patterns with the remainders.

Children also see connections between equations. For example, they will recognize that 17 divided by 2 is 8 R1 and 17 divided by 8 is 2 R1, and that this relates to 2 x 8 = 16. As children become comfortable with this string of division questions, we start to find decimal and percent equivalents for some of the fractional remainders. Long division is often a tricky concept for junior grade students. It is my hope that using relatively small numbers during the DMD will help children later when they are working with larger numbers.

In the examples above, students systematically divide the school day number by numbers 1 to 10. The goal is to identify the equations that yield whole numbers, directly connecting to their work with factors.

January/February: Fractions and Place Value

Fractions

After the holiday break, the focus shifts to fractions. We work with the day’s number in two ways, depending on whether the number is a prime or composite number. For a composite number, such as 48, I ask the children to figure out fractions of 48 (Fig. 6). Children notice doubling and halving relationships, they work with equivalent fractions, and they are challenged to think about whether a fraction is more or less than 1/2. If the day’s number is a prime number, we work with it in a different way. The number is, instead, the answer to each equation. They must think of a number the day’s number would be a part of. For example, on Day 48, children might be asked, “½ of what is 43?” (see Fig. 6).

Throughout this process, I ask children to explain their thinking with the question “How do you know?” I also ask them to share any relationships they notice between the equations. I find that diagrams showing fractional parts can be helpful here. For example, a circle divided into 4 with each part worth 43 can help children to see that the total would be 172 when asked ¼ of ___ = 43 (see Fig. 7).

(Fig. 6) For composite numbers, students determine fractions related to the number.

(Fig. 7) For prime numbers, students determine a fraction related to the school day number.

Place Value

As I am currently teaching a grade 4/5 split class, I’ve added a new focus in the winter term on place value for my younger students. We work with the digits in today’s number, creating a list of numbers that range from the hundred thousandths to the millions. The numbers are written in an organized fashion so children can see how the place value of a number affects its value. The foray into decimals was initiated by a student who wanted to turn 93 into 9.3 and .93. We work on expressing decimals in a way that indicates their meaning – “9 and 3/10” and “93 hundredths” rather than “9 point 3” and “point 93.”36

March/April: Multiplying and Dividing by Multiples of 10

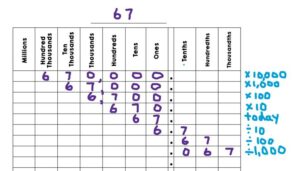Our spring focus is on multiplying and dividing the day’s number by multiples of 10. A place value chart is used as an organizer so children can see how the result is bigger or smaller after the number is multiplied or divided (see image). The children also practise reading decimals in a meaningful way: 2.4 is “2 and 4 tenths”, 0.24 is “24 hundredths”, and 0.024 is “24 thousandths.”