Hundreds of studies across a variety of contexts have demonstrated the unique capacity of number line models to ground student understanding of numerical quantities and relationships. Number lines make explicit and build upon pre-existing spatial-numeric intuitions, support children’s growing understanding of ratio, proportion and scaling, and help students to construct and internalize a “mental number line” that continues to develop in complexity from kindergarten through university mathematics and beyond.
A glance at recent Robertson newsletters shows the prominence of number lines in children’s math learning, including the engaging game of “Fraction Ball” (Feb. 2023) or fifth graders’ discussions of number concepts based on the calendar (April, 2023). Number lines also make an appearance in past Robertson discussions of games, symmetry, and early assessment, among other topics.
Of all the early assessments, children’s ability to accurately map numbers onto a number line most robustly predicts their achievement in mathematics, says cognitive psychologist Zachary Hawes at the University of Toronto. Even the deceptively simple task of placing a few whole numbers on a blank line bounded at each end with a benchmark number (0 and 10, for example) has remarkable predictive power for a child’s later understanding of advanced number concepts.
Yet, despite overwhelming expert consensus that number lines can play a powerful role in math education, the model also presents unexpected challenges for students of all ages. Teachers quickly come to recognize that number lines do not offer a transparent or seamless bridge between implicit numerical intuitions and explicit or effortful mathematical reasoning. Probing the nature of a child’s number-line difficulties can offer a teacher valuable insight into their conceptions, misconceptions, and partially developed conceptions of number and space, and how the two come together.
What is a number line?
A number line is essentially a linear spatial representation which supports students’ grasp of numerical order and magnitude. Sorting quantity and data into linear space, the number line makes visible the connections between measure and number, and helps to build understandings of place value and proportional reasoning.
“There are things the number line affords that other representations don’t,” Hawes explains. “It’s a tool that provides insights into different aspects of mathematical thinking, like understanding the unit, and how to divide up space to impose the unit. It’s also one of the only representations early on that allows children to see number applied to continuous space in terms of measurement. We tend to be preoccupied with counting discrete objects, but with a number line we can appreciate and move towards a more continuous and proportional way of thinking about number. This is really useful. It’s key to understanding fractions and other higher level math concepts.”
Number line models also lay the ground for the move from one-dimensional (linear) space to two-dimensional (and, eventually, higher-dimensional) representations of algebraic functions as defined by perpendicular axes in a coordinate plane.
Types of number lines
In elementary classrooms, number lines assume a vast variety of forms, depending upon their purposes and the developmental level of students. They include linear arrangements of countable objects (such as abaci, bead strings, or Rekenreks), number paths with countable spaces, number lines evenly subdivided with marked numbers, empty number lines requiring users to subdivide them to solve designated problems, “double” number lines that support work with ratio, proportion, and algebraic equivalence, and “variable” number lines reflecting algebraic relationships. Empty number lines appear to offer especially flexible models, both for working with a range of mathematical ideas and for revealing student understandings and misunderstandings (see, for example, “The Empty Number Line: A useful tool or just another procedure?”, Teaching Children Mathematics, 2009).
Some teachers use vertical number lines in addition to horizontal ones. Advantages of this practice include the following considerations: (a) It builds flexibility and helps to forestall the reification of a single representation as the way numbers actually are (b) Vertical lines reflect everyday metaphors of magnitude in terms of height; (c) Working with horizontal and vertical number lines supports graphing from kindergarten bar graphs to work with coordinate grids. It can also be difficult for some children to reconcile the left-to-right directionality of horizontal number lines with right-to-left place-value conventions for written numerals.
Certain manipulative materials, such as unidimensional (Unifix) linking cubes, support a linear understanding of number and possibly help students transition between discrete and continuous views of numbers. One interesting curriculum, Learning Mathematics through Representations (UC Berkeley), integrates number lines with the use of relational (Cuisenaire) rods. Rulers and measuring tapes are based on number lines, and many of the measurement misconceptions exhibited by children parallel their difficulties with number lines in general. (Promising measurement strategies such as the use of a “broken ruler” (e.g., Drake, M., 2014) may equally apply to number line understanding). Adaptations of number line concepts are also evident in tools such as 100s charts or calendars. Many board games are structured as number paths, and the work of Siegler and Ramani (2009) has shown the effectiveness of simple board game interventions on math skill (with the interesting caveat that the path must be linear rather than circular).
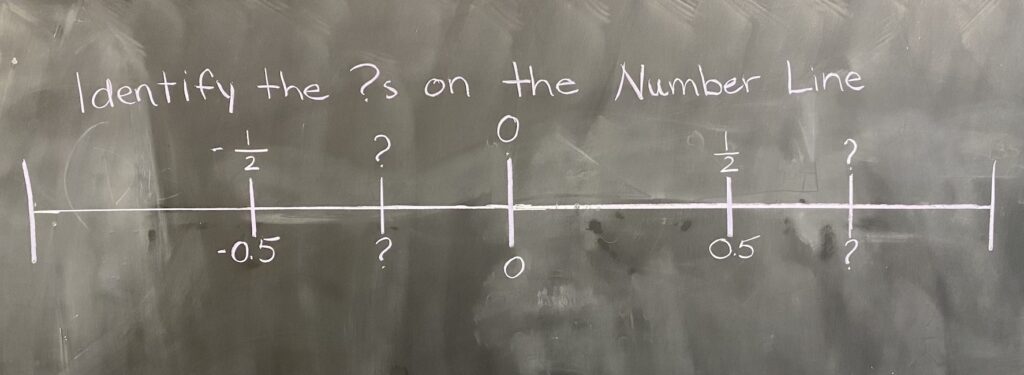
The number line – a conceptual tool that allows for numbers to be conceived as locations along a line mapping numerical difference onto difference in spatial extension… is mathematically simple, yet it is extraordinarily powerful. (Nunez, 2017)
Number Line Activities
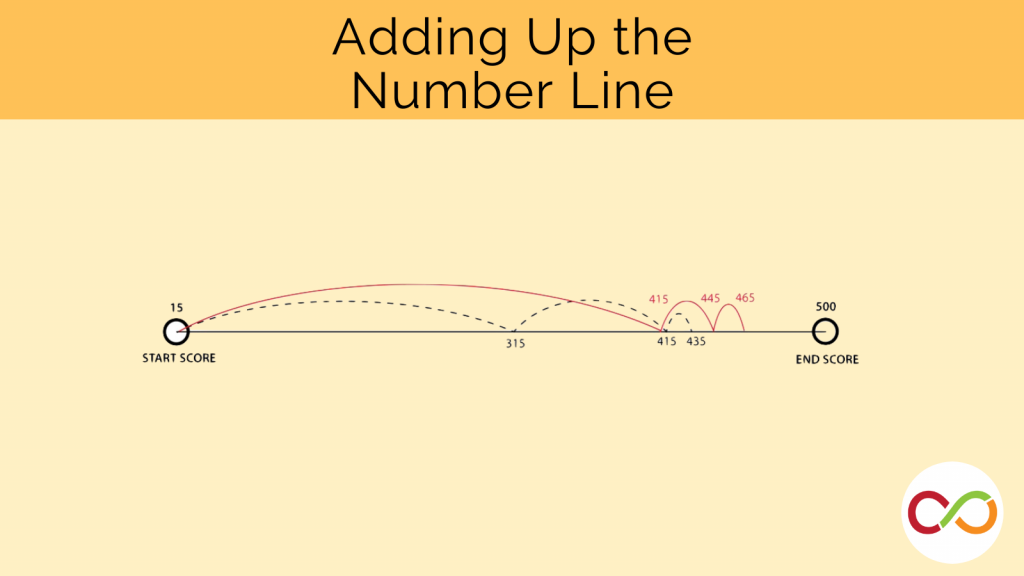
In this addition and subtraction game, students attempt to arrive exactly at 500 on the number line.

Students use a number line to explore the relationship between fractions and their equivalent decimal forms.
"Broken Ruler" Activity

Students measure objects with a ruler, but they can’t start at 0 cm!
In Singapore, math learning is supported across the grades through the use of number bars, a versatile tool closely related to number lines. This short video offers an elegant example of number bars used in algebraic problem-solving.
Number lines as cultural tools
In the industrialized world, number lines are all around us. We encounter them in an array of measuring and navigation tools (rulers, calipers, maps, highways with mileage markers, thermometers, scales, and so on.) Linear unit-based organizing systems also appear in connection with timelines, calendars, timekeeping devices, musical notation, and urban house addresses. While we might wonder how the shift from analog to digital devices may have affected contemporary children’s intuitive grasp of proportional linear models, it’s possible that this development has been amply counterbalanced in children’s lives by the rapid proliferation of quantitative graphic information of all kinds. Regardless, students benefit from explicit comparisons of the affordances and constraints of different visual-spatial models as organizers of quantitative information and tools for reasoning about it.
Disentangling culture from development is challenging, and the role of culture in developing a directional mental number line has been vigorously debated (e.g., Dehaene, 1997; Nunez, 2016; 2017; Pitt et al., 2021). There is evidence that very young infants and certain non-human animals possess innate spatial intuitions of magnitude that increases in a left-to-right direction, while other work shows that number line orientations depend upon the writing conventions of the culture. Ethnographers have also identified Amazonian Indigenous communities in which the spatialization of number appears to be either absent or lacking consistent directionality. Some Australian educators have argued that number line metaphors may be inappropriate for students who speak Indigenous languages with verb-based number concepts. (Edmunds-Watham, C., 2012)
Development of number line concepts
Early childhood teachers note many precursors to linear representations of number in children’s play. Along with spontaneous sorting, sequencing by size, and patterning, young children are commonly observed to line things up and exult in how far the line extends. This linear organization of objects facilitates accurate counting with its clarification of starting points and endpoints. It also may elicit intuitions of infinity; as one kindergarten child remarked as she traversed the classroom carpet with a long line of cubes, “If we had enough blocks, my pattern would go on forever, even to the end of the world!”
At the same time, many young children are just mastering the idea that numbers are for counting discrete things, with associated ideas of one-to-one correspondence, stable counting order, and cardinality. In this context, the abstractness of a classic number line that represents numbers as dimensionless points rather than countable objects can be confusing. According to the 2009 National Research Council Report Mathematics Learning in Early Childhood, “young children have difficulties with the number line representation because they have difficulty seeing the units – they need to see things, so they focus on the numbers instead of on the lengths. They may count the starting point 0 and then be off by one, or they focus on the spaces and are confused by the location of the numbers at the ends of the spaces.” Number line ordering conventions may also clash with a child’s recently acquired understanding that the order in which you count things makes no difference to the outcome.
For these reasons, some teachers opt to introduce bead strings or number paths as transitional models that better mesh with their students’ developmental levels of understanding. A number path, for instance, offers a sequence of countable squares. It supports one-to-one correspondence as a child places objects within the squares or counts back and forth among them. The tool also reinforces ideas of cardinality and supports other useful strategies such as counting on from a given number.
Although in many ways number paths seem well-positioned to lay the ground for grasping the abstractions of a continuous number line, it’s a notable conceptual leap to move from something concretely countable to a qualitatively different way of thinking about number. Shifting focus from the spaces to the boundaries between the spaces (hash marks) raises challenges that are far from trivial. A recent article in the NCTM journal Mathematics Teacher: Learning and Teaching PK-12 (Peyser and Bobo, 2022) offers some useful strategies for supporting this transition.

Children from Pegamigaabo School in Big Grassy First Nation see how far they can extend a line of multilink cube towers.

A child from Pegamigaabo School in Big Grassy First Nation lines up progressively taller multilink cube towers next to their corresponding number.
“I once worked with a group of teachers whose students were really struggling with number lines, especially when they used them as arithmetic tools. It had to do with how they were counting – lots of students just count the hash marks. It’s not a reason not to use it, though – if anything, it tells you that they still aren’t really understanding what the number line is conveying,” Dr. Hawes recollects. “I’m leery of the number line at times because I think people overuse it and don’t always understand why it’s useful. It becomes another tool that becomes proceduralized and you stop making sense of the number relations. In one classroom, they always used the same scaled number line. When the kids used a differently scaled number line, they weren’t able to scale one number line to another in terms of numerical relations. They memorized the order of numbers but weren’t paying attention to the proportionality, the scale.”
These examples reinforce the importance of working with (and translating among) differently scaled number lines to focus on the structural relationships that remain invariant through scale transformations. “You could use a human number line, for instance. If one kid stands here, and it’s 0, for example, and someone else stands here, on number 125, where would 50 be? Now let’s shrink everything – as the kids move closer together, where is 50 now?” Hawes suggests.
The flexibility to shift among scales is most easily developed using simple, open materials that allow for unencumbered positioning and repositioning of numbers, such as placing cards along a designated line or clipped to a string as suggested on the Clothesline Math website. Their activities are thoughtfully designed to accommodate growing mathematical complexity. Virtual number lines may offer similar advantages.
Another developmental challenge is that children’s internal models of numerical distance don’t perfectly fit the evenly spaced unit mapping offered by the number line. Asked to place numbers along an unmarked line, even older children show a strong tendency to order them logarithmically rather than linearly, with numbers crowding closer together as they get larger.
This distance effect, in which the difference between two and four, say, is perceived as exponentially greater than the difference between 98 and 100, appears to be strong and enduring. Even adults tend to revert to logarithmic models when dealing with very high numbers.
Beyond the countable: Extending the number system
Tangible physical materials may be well suited to support early understandings of the natural (counting) numbers, but it’s harder to make sense of integers that include negative numbers, which represent absence.
As we can see from the example on the right, the mirror symmetry that obtains between negative and positive integers along a number line may be less than obvious to a child.
Examples of this sort serve as reminders that explicit teaching and learning are required to bring out the structural concepts embedded within a mathematical model. In this case, the researchers focused on helping students notice the inherent symmetry of integers around the zero point, with the aim of integrating symmetry structures with other number line properties such as order and magnitude. Incorporating bodily/perceptual elements through a folding number line, their curriculum prompted children “to notice symmetry in the integers, integrate symmetry with other properties of integers, and internalize these structures into their mental representations of the integer number system.” (p. 159) Adapted for this purpose, the number line proved to be a generative model on which to hinge fundamental understandings of positive and negative integers.
Visualizing Integers
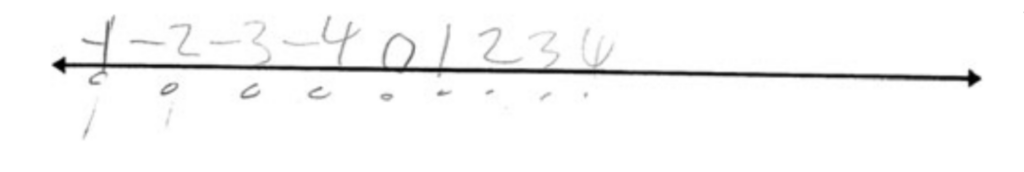
We can see how the production of a typical fourth grader failed to recognize the structural properties of the integer sequence (example from Tsang et al, 2015).
Zooming in: Making room for fractions
The magnitudes of all rational numbers are represented on a mental number line, a dynamic structure that begins with small whole numbers and over the course of development expands rightward to include larger whole numbers, leftward to include negative numbers, and interstitially to include fractions and decimals … Viewing the mental number line as a dynamic structure that can represent all numerical magnitudes allows the integrated theory to extend from infants’ representations of non-symbolic numerical magnitudes to young children’s representations of symbolic whole number magnitudes to older children’s, adolescents’ and adults’ representations of symbolic fraction, decimal, and negative magnitudes. (Siegler, 2016)
As suggested by Robert Siegler, a prominent math researcher and number line advocate, the power of the number line lies in its capacity to incorporate increasingly complex ideas of number. It is well documented that the introduction of fractions often constitutes a discouraging mathematical turning point for children. Elementary pedagogy tends to stress area models, which link nicely to experiential intuitions of fractions as part-whole divisions. For fuller understanding, though, students must also come to see fractions as numbers in their own right, with magnitude that can be represented as evenly ordered points along a line in relation to other numbers. Broadening fraction concepts using number lines potentially alleviates persisting confusions associated with over-reliance on iconic part-whole images (such as pizzas) in classrooms.
The video on the right from the Clothesline Math site shows a teacher introducing fractions on a number line to young high school students. In our own practice, we’ve repeatedly seen how the seemingly basic task of ordering fractions and decimals along a number line – whether in later elementary years or in teacher education classes – poses productive challenges and generates discussions that get to the heart of number understanding. Research has demonstrated the effectiveness of using number lines to both assess and increase fraction magnitude understanding for struggling math students (Gersten, Schumacher and Jordan, 2017 – for more on this topic, see the special (2017) issue of the Journal of Learning Disabilities).
Students are also fascinated to realize, not only that number lines extend infinitely in both directions, but also, that – given any two points along the line – they can always find a number that fits between them. Virtual dynamic lines – such as seen here – can help to bring this to life.
Educator Chris Shore demonstrates how he introduces fractions on a number line to young high school students.
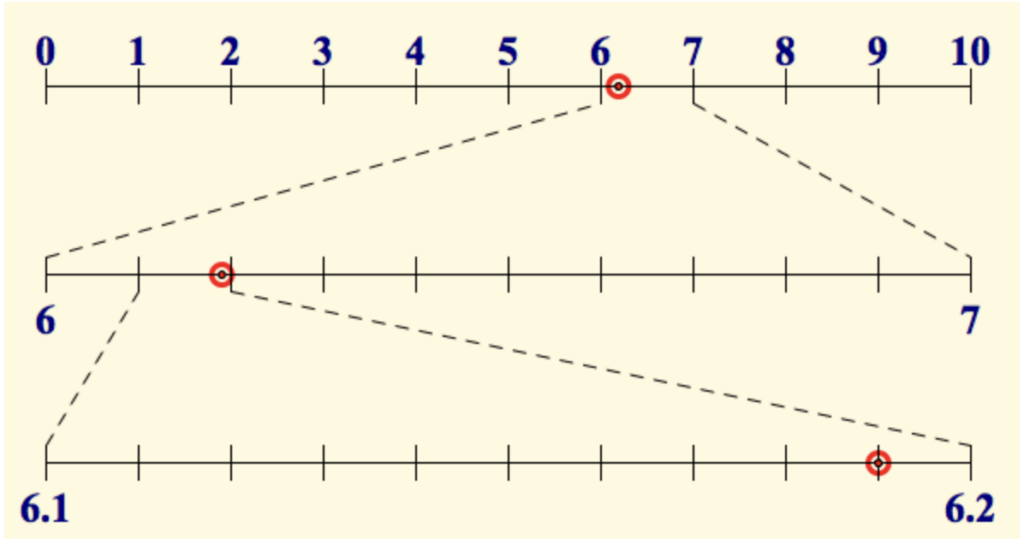
Number lines extend infinitely in both directions and a “new” number can always be found between any two given points along the line.
“Walking the Number Line”: Embodied Cognition
There is growing evidence that many abstract mathematical ideas are based on sensory/perceptual experiences involving bodily movement through space.
Any representation of quantitative difference as linear distance implies associated metaphors of time and motion. We see more direct mathematical embodiment in very young children who have just mastered the counting sequence as they march down the hallway or up the stairs vigorously chanting the count for each step they take. One three-year-old tripped on the stairs and, on being consoled by his parent, sobbed “Number 3 was too steep.”
A study out of Germany (Link et al, 2013) compared the effects of two number line interventions on the mathematical improvement of first graders. One condition offered conventional number line training which asked children to indicate the position of a number on a tablet-based number line. The other (embodied) condition instructed children to walk along a physical line on the floor until they reached the target number’s estimated position. The effects of the number line training were generally stronger in the embodied condition. In particular, skill in single-digit addition improved for the walking but not the tablet group.
It has been suggested that embodied number line interventions may have especially strong impacts on children with math difficulties.
Embodiment may also account in part for the success of the “Fraction Ball” adaptation of basketball described in Bustamente et al. (2022; see Robertson blog Feb/2023). The encouraging results suggest many easy possibilities for teaching, ranging from various forms of hopscotch to improvised dice games in which students physically move forward and backward along a number line (using one die for number and the other for direction). The height metaphor that imbues our everyday talk about numbers is further concretized and internalized by moving these games to the stairs and can be extended into negative numbers by heading to the basement.
Growing with the number line

In the game Fraction Ball, students use a court-side number line during to keep track of their team’s score.

Some forms of hop scotch can be considered a number line.
Speaking with Zack Hawes, it’s clear that we have only begun to touch upon the rich potential of this everyday classroom prop. “The number line is such a great way of thinking about number. It maps perfectly onto fractions, and you can scale it up the grades. It’s a representation you can carry with you. The more you think about it, the more you realize how brilliant it is. Such an interesting use of space to organize ideas and relations!”
References
Bobis, J. (2009). The empty number line: A useful tool or just another procedure? Teaching Children Mathematics, 13, 410-413.
Bustamente, A.S. et al. (2022). Fraction Ball: Playful and physically active fraction and decimal learning. Journal of Educational Psychology, 114, 1307-1320.
Edmunds-Watham, C. (2012). Spatial metaphors of the number line. In J. Dindyal, L. P. Cheng & S. F. Ng (Eds.), Mathematics education: Expanding horizons (Proceedings of the 35th annual conference of the Mathematics Education Research Group of Australasia). Singapore: MERGA.
Dehaene, S. (1997) The Number Sense: How the Mind Creates Mathematics, Oxford University Press.
Drake, M. (2014). Learning to measure length: The problem with the school ruler. Australian Primary Mathematics Classroom, 19, 27-32.
Gersten, R., Schumacher, R.F. & Jordan, N.C.(2017). Life on the number line: Routes to understanding fraction magnitude for students with difficulties learning mathematics. Journal of Learning Disabilities, 50, 655-657.
Link, T. et al. (2013). Walk the number line – An embodied training of numerical concepts. Trends in Neuroscience and Education, 2, 74-84.
Nunez, R. (2017a). How much mathematics is hardwired if any at all? Biological evolution, development, and the essential role of culture. In M.D Sera, S.M. Carlson & M. Maratsos (Eds.), Minnesota Symposium on Child Psychology, 38, 83-124. John Wiley & Sons.
Nunez, R. (2017b). Is there an evolved capacity for number? Trends in Cognitive Science, 17, 409-424.
Peyser, E. & Bobo, J. (2022). Linking number sense to linear space. Mathematics Teacher: Learning and Teaching PK-12, 115(2), 113-121.
Pitt, B. et al.(2021). Spatial concepts of number, size, and time in an indigenous culture. Science Advances, 7, 1-6.
Siegler, R. S. (2016). Magnitude knowledge: The common core of numerical development. Developmental Science, 19(3), 341-361.
Siegler, R.S. and Ramani, G.B. (2009). Playing linear board games – but not circular ones – improves low-income preschoolers’ numerical understanding. Journal of Educational Psychology, 10, 545-560.
Tsang et al. (2015). Learning to ‘see’ less than nothing: Putting perceptual skills to work for learning numerical structure. Cognition and Instruction, 30(3), 154-197.

