A parent recently told me about her child in Grade 3 who was struggling to identify how many hundreds, tens, and ones were in any given number. “Is this necessary? What’s the point?” the mother asked me.
Children often learn about place value in the context of subtraction1. Subtraction of two-digit numbers may require re-grouping (sometimes described as “borrowing”). Some children learn these procedural skills without a clear understanding of what “borrowing” really means. This is a problem for the overall conceptual understanding of numbers2. A solid understanding of place value helps children understand that the position of a digit in a number determines its value. This understanding is crucial for all mathematical operations3 and can help children break down complex problems into simpler parts, making them more manageable4.
There are many ways to practice becoming fluent with place value and understanding the relationships between digits. But I’m going to explain the only game you need to know to teach place value! Just kidding – there are many. But this is a pretty good one!
Closest To
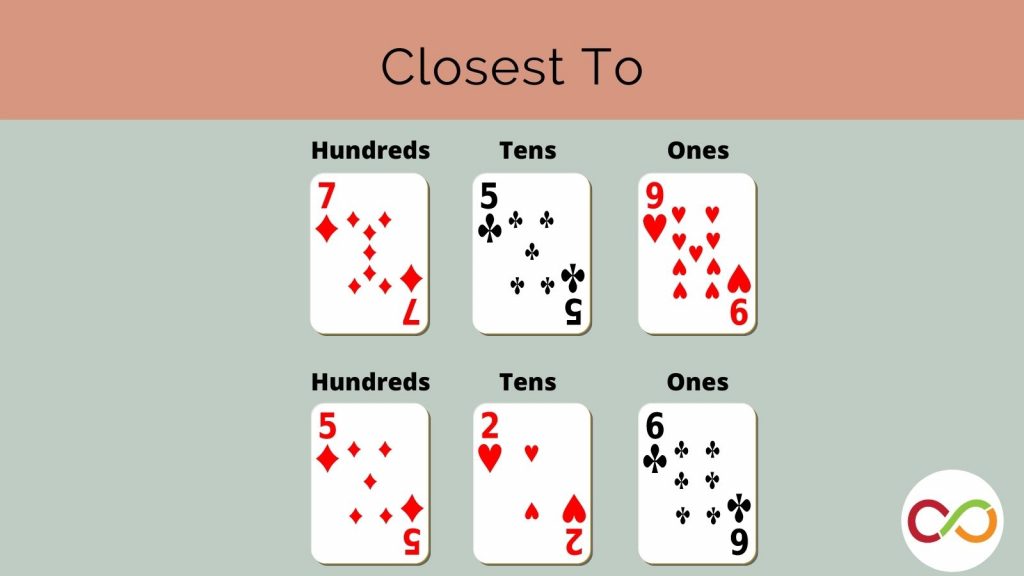
The game “Closest To” is my favourite place value game because it is easily adaptable and requires just a deck of cards. The simplest form of this game asks children to make the biggest (or smallest) number out of two cards. For example, if a child receives a 3 and 7, they can make the number 37 or 73. This gives you the opportunity to draw attention to the numbers in the tens and ones place value. If you’re recognizing that the child is beginning to understand place value, you can ask, “What is the value of the number in the tens column?” For example, when working with the number 37, the value of the number in the tens column is 30. You can also ask, “How many tens are there?” In this case, there are three tens. Students can be asked to represent these numbers symbolically (e.g., numbers) or non-symbolically (e.g., base-ten blocks).
More complex versions of “Closest To” can require students to extend their thinking about place value into the hundreds and thousands. The game can even extend to learning about decimal place values like tenths or hundredths! To increase engagement (and excitement), I deal out cards one-by-one and ask children to place that card in the ones, tens, or hundreds section. This allows for discussions around why placing a 9 in the hundreds column and a 2 in the ones column are good choices when trying to create the largest number. As the game continues, we discuss what number needs to be revealed to win the game.
You can also include operations (adding, subtraction, multiplication, and division) by challenging students to reach a target number when playing multiple rounds. Children can also be asked to think about their numbers in standard, expanded and word form to emphasize how numbers can be expressed in different ways.
The best part of this activity? It’s fun while also helping children build and practice a foundational understanding of numbers!
Access a complete lesson plan with curriculum connections and printouts that help students place cards in the place value position of their choosing.

Dr. Larisa Lam
Director, The Robertson Program for Inquiry-based Teaching in Math and Science
Related resource: Place value assessment
Use a set of identical blocks to help determine the place value number knowledge of your early years students.
References
1. Fuson, Karen C., and Diane J. Briars. “Using a base-ten blocks learning/teaching approach for first-and second-grade place-value and multidigit addition and subtraction.” Journal for research in mathematics education 21.3 (1990): 180-206.
2. Baroody, Arthur J. Children’s mathematical thinking: A developmental framework for preschool, primary, and special education teachers. Teachers College Press, 1987.
3. Siegler, Robert S., and Patrick Lemaire. “Older and younger adults’ strategy choices in multiplication: testing predictions of ASCM using the choice/no-choice method.” Journal of experimental psychology: General 126.1 (1997): 71; Kamii, Constance, and Linda Joseph. “Teaching place value and double-column addition.” The Arithmetic Teacher 35.6 (1988): 48-52.
4. Stein, Mary Kay, and Jane W. Bovalino. “Reflections on practice: Manipulatives: One piece of the puzzle.” Mathematics Teaching in the Middle School 6.6 (2001): 356-359.