While working with educators to develop new ways to teach spatial reasoning to early years’ students, The Robertson Program met Jane Tom, an educator at Pegamigaabo School in Big Grassy First Nation. Jane was eager to try new ways of engaging her students in math. She quickly took to the lessons we introduced to her during professional development and began adapting them to better suit the needs of her students.
One major change Jane made was to her morning routine: She began each day with a quick image math challenge. Jane would briefly show the Grade Ones and Twos an image or set of images of math manipulatives on her SmartBoard. The students would then have to visualize how to transform the image in some way and replicate the change using real math manipulatives at their desks.
“When we do the challenges, I notice how happy the kids are, how engaged they are, and how comfortable they are,” Jane says. “They aren’t threatened by it at all. It’s really a lot of fun for them.”
Quick Image Challenges became a staple in the spatial work we were doing because they can be incorporated into any math class. They can be adapted to meet the needs of students, they lend themselves to many areas of mathematics, and students enjoy working on them. Moreover, the challenges allow for multiple entry points to learning so educators can meet students at varying levels of ability.
The challenges are also intended to be repeated over time, allowing teachers to revisit and review concepts, perhaps increasing the difficulty each time.
“People retain information better when everything is not learned at once, in one long sitting. Learning improves when it’s spread out over time,” says Dr. Zack Hawes, Robertson research lead and OISE mathematics professor. “By breaking down the learning into smaller, concentrated periods of practice, students benefit because it allows for the building of knowledge on an ongoing basis. An approach that is referred to as distributed practice or spaced learning.”
Watch Jane's Class Engage in Quick Image Challenges
Jane Tom leads her class in a series of three quick image challenges at Pegamigaabo School in Big Grassy First Nation
When the Robertson Program conducted spatial reasoning research in 2017, we considered how repeating activities over time might influence learning. We concluded that repeated challenges may provide children with meaningful context to develop an understanding of number concepts and their various relations. Moreover, it’s possible the repeated experiences of relating number words with various spatial representations was helpful in the acquisition of symbolic number understanding (e.g., reading and writing numerals) in learning contexts outside the study1.
“Rather than only learning geometry and spatial sense in June, you’re now learning slowly and building your spatial reasoning throughout the year, allowing for more connections to other aspects of mathematics to be made along the way,” says Hawes. “For example, in Square Moves, when students move a square in one image to make it look like another image, they see how it actually lends itself to measurement.”
The short timeframe of the challenge is also significant because it requires intense concentration from students for only a brief amount of time.
“Capping the challenge off at 15 minutes or so is an important aspect because it keeps student engagement and motivation high. Students often leave wanting more,” Hawes says. “And they’ll get more when you return to the challenge in a few days. These are not easy challenges. They are not boring. They should lie somewhere in between, challenging students to engage in spatial reasoning in fun but rigorous ways.”
If the challenge is beyond the students’ level of comprehension, it isn’t effective. Educators will need to adapt activities to make them level appropriate. However, because these activities are providing educators with an opportunity to observe how their students respond to specific math challenges, the educator can react by adapting or addressing an area of struggle that may otherwise have gone unnoticed.
“You as the educator have to take the quick image activity, be critical of it, see what it can afford your students and then adapt it depending on what you want to get out of it,” Hawes says, noting the challenges created by the Robertson Program are all spatial and easily adaptable. “A lot of these activities can be scaled up or down. It doesn’t matter where you start, necessarily – as long as you’re responding to the needs of your students.”
That’s what made the quick images so appealing to Jane.
“Everything that was introduced to the students, made so much sense to me. I took the ball and ran with these challenges,” she says. “It is such a wonderful feeling that I can’t put in words.”
Hawes suggests Can You Draw This as an initial activity that can be tailored to student needs. Students are briefly presented with a geometric design (for about 5 seconds) and then must recreate/draw the design from memory. The activity provides students the opportunity to use and hear spatial language and notice key geometric properties and spatial relationships. The activity also easily lends itself to other mathematical topics and discussions, such as symmetry, measurement, fractions, and proportional reasoning.
Recommended by Dr. Zack Hawes
When students compare two different areas, many will be formulaic about it. But another powerful approach is determining whether one can transform into the other. This activity demonstrates how a portion can be removed from the shape and relocated to create a new shape that takes up the same amount of space.
How do you get from one shape to the other? This activity examines the relationship between two variables or, in this case, the relationship between two shapes. Student will begin to recognize transformation and change – the foundation for many areas of math. You can also look at rotations or translations.
“You can turn Can You Draw This into a fraction talk,” he says. “You start off with the drawing task, then move into a discussion about fractions. How much of the whole shape or image is represented by the triangle? What about the square? How can you prove this?”
Finally, because the quick image challenges are an individual task, but take place collectively as a group, educators may recognize mathematical strengths in students that were previously unknown. Jane Tom remembers seeing her students in a different light.
“One moment that stands out to me has to do with a student of mine who always had a little bit of a difficult time catching on to new things in math and literacy. But with quick images he was so successful,” she says. “I liked doing the challenges to just give him that confidence in himself.”
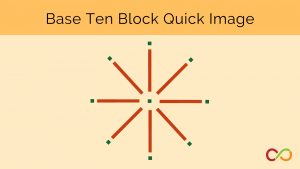
Base Ten Blocks
Students recreate – from memory – an image composed of base ten blocks. They then calculate the sum of the values of each block.
Multi Link Cubes
Students visualize 2D images of 3D shapes made up of multilink cubes. They then recreate the arrangement from memory.
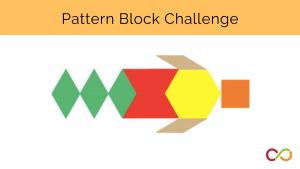
Pattern Blocks
Students are quickly shown arrangements of pattern blocks. They then recreate the arrangement from memory.
Can You Draw This
Students combine art with math to express knowledge of spatial language and geometric shapes.

Zachary Pedersen
Program Coordinator, The Robertson Program